Resources

About

SmartBuildings is the database of a company wihch deals with the construction and renovation of buildings with the purpose of improving their structural health and overall safety

Highlights

Calculate the area of any given building

Walls are stored as segments in the Euclidean plane {(X1, Y1), (X2, Y2)}, this means that using the shoelace formula it is possible to calculate the area of any given building, and in the database there is a function which does just that

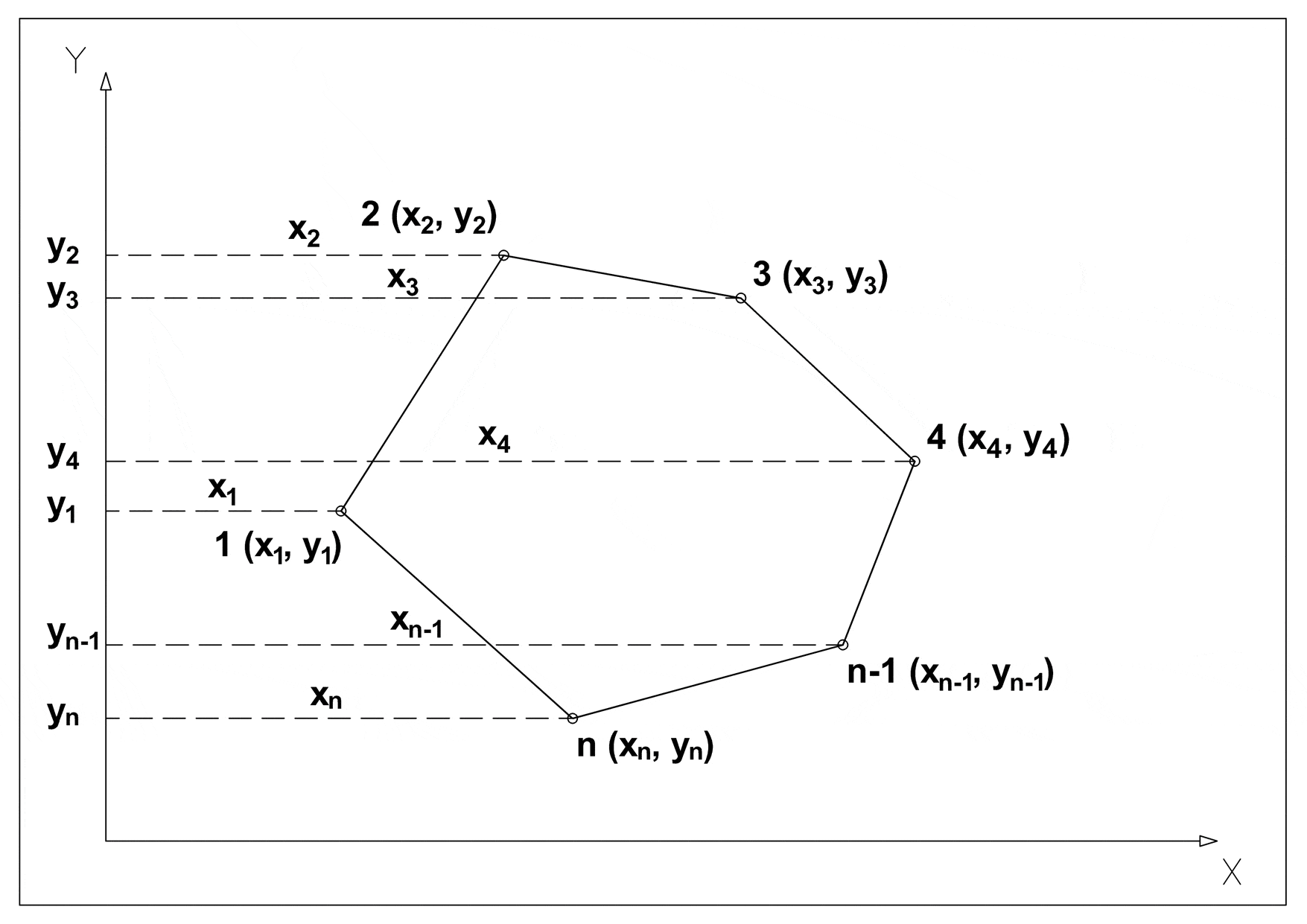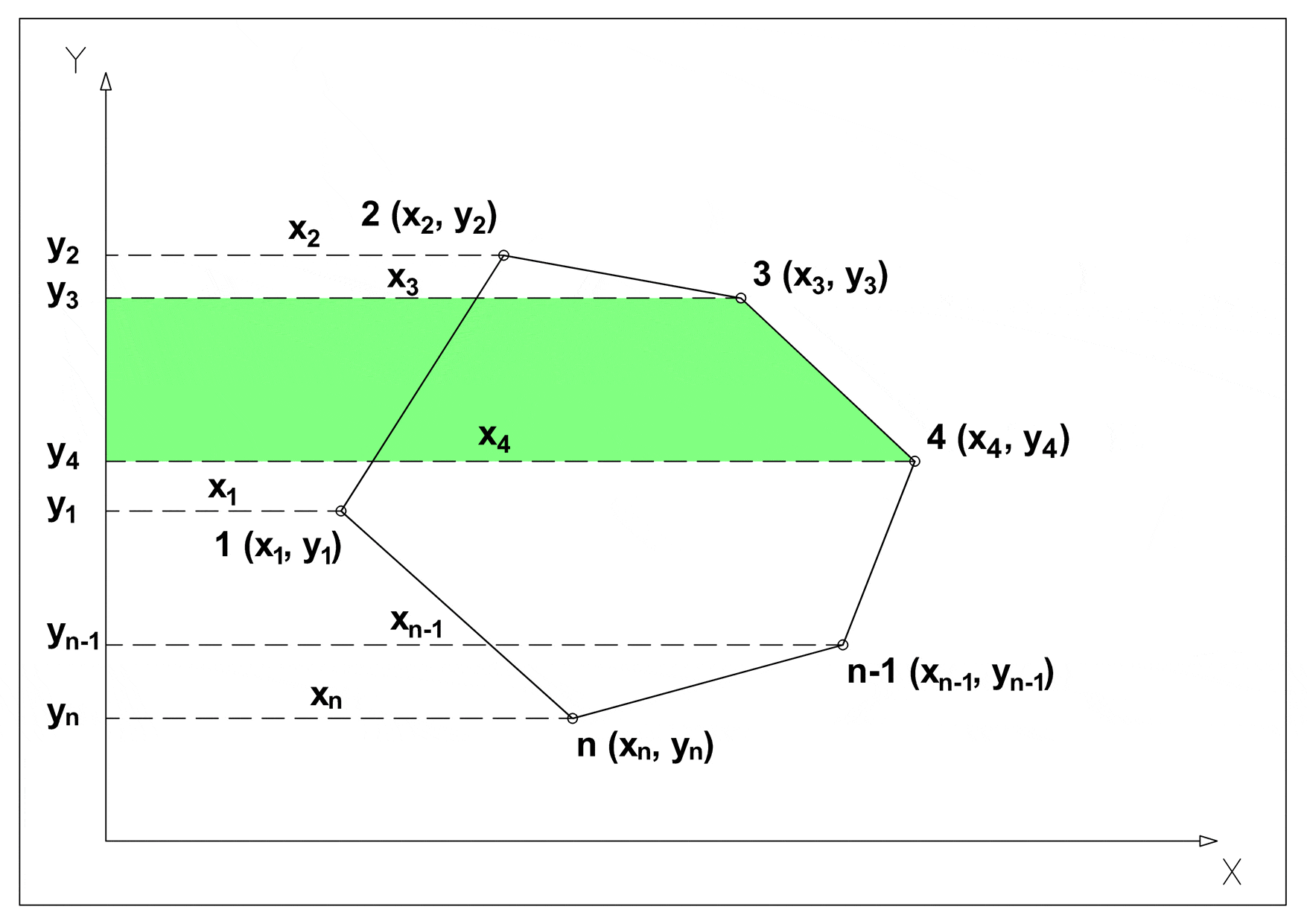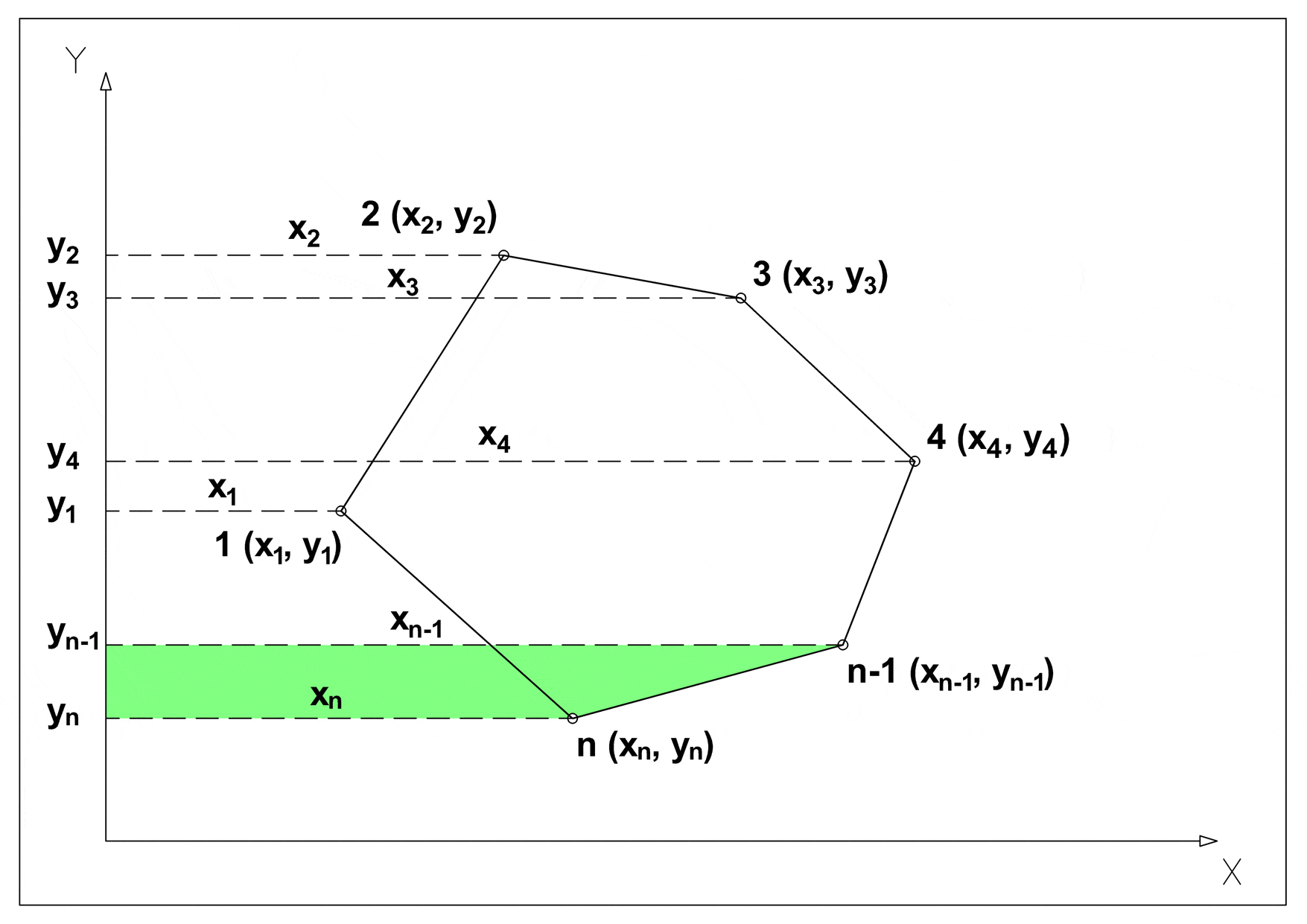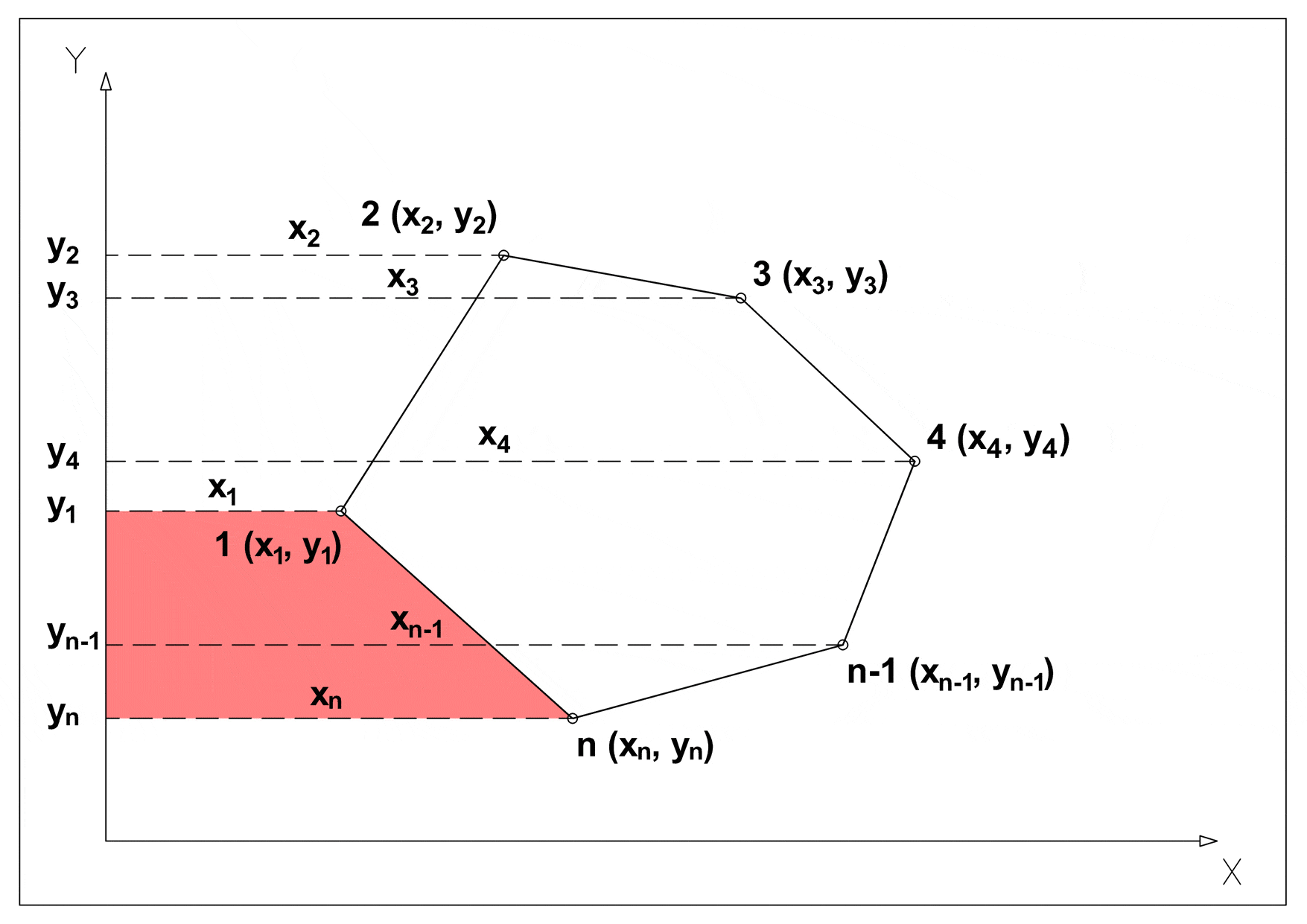
Shoelace formula animation

In order to apply the shoelace formula we must:

  1. Only consider the polygon formed by the external walls of the building (trivial: an external wall is a wall that delimits one and only one room)
  2. Order the vertices of that polygon in either a clockwise or counterclockwise order

To achieve the second point, one can simply start from a random vertex of the polygon and then query the table containing the walls to get (one of) the two adjacent vertices. By keeping track of which vertices have already been visited, one will end up with either a clockwise or a counterclockwise ordering, depending on the random choice made at the first vertex

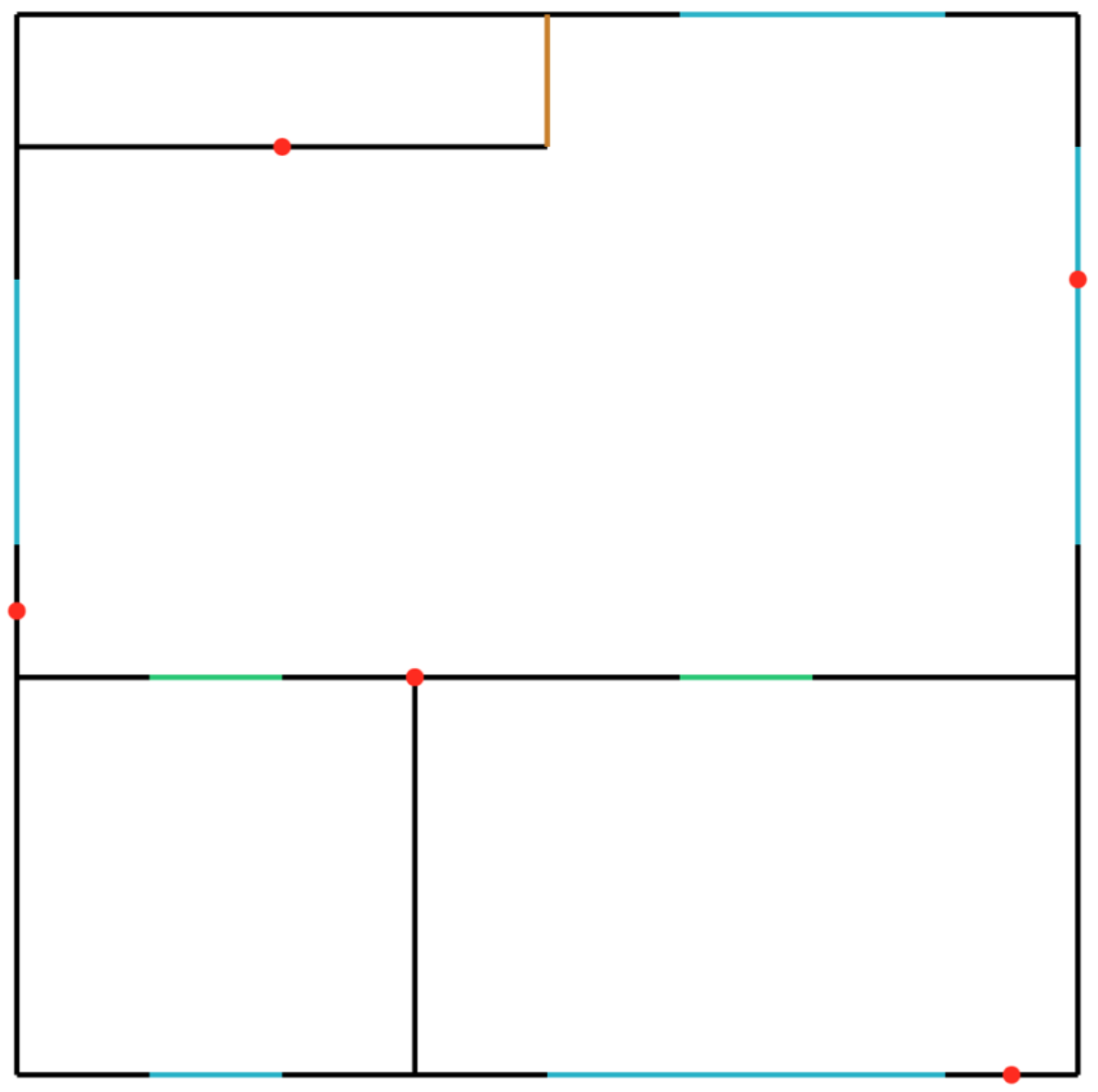
Create an SVG plan of any given floor

The database contains a function which outputs a string representing the SVG plan of any given floor:
  • Blue segments are windows
  • Green segments are doors
  • Brown segments are generic openings
  • Red dots are sensors
Floor plan

Estimate the magnitude of an earthquake

In case of an earthquake, a database administrator can launch a stored procedure that estimates its magnitude using data gathered from the accelerometers of nearby buildings

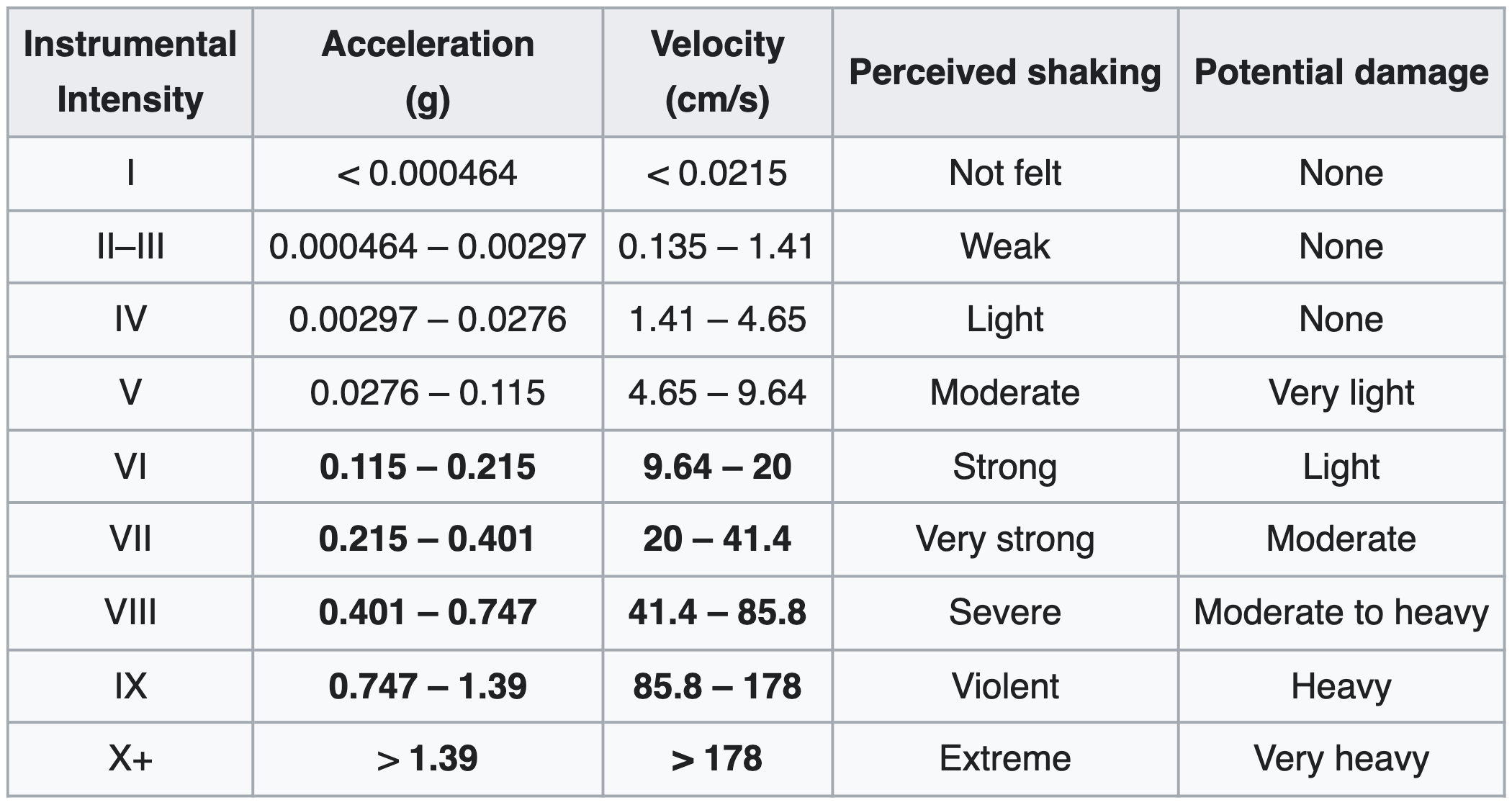
First, every (nearby) building computes a rough estimate of the magnitude by mapping the average measured acceleration to a magnitude value of the following table:

PGA to Mercalli table

Then, all the perceived magnitudes are used to approximate the intensity of the earthquake in its epicenter \(Mercalli_0\) by inverting the following (heuristic) formula:

\[ Mercalli(r) = \frac{Mercalli_0}{\left(\frac{r}{\mu} + 1\right)^2} \]
  • \(Mercalli(r)\) is the perceived magnitude of a building distant \(r\) km from the epicenter
  • \(\mu\) is the attenuation coefficient of the mechanical waves coming from the earthquake, by default 600
  • \(+ 1\) stops the function from going to \(+\infty\) for \(r\to0\)
  • The exponent 2 at the denominator accounts for the fact that the energy carried in mechanical waves attenuates quadratically with the distance from the epicenter